Algorithm of solving the linear equation ax + b = 0

Our task is to find the solution to a linear equation. The general form of a linear equation can be written as follows:

ax+b=0

where a and b are known real numbers, called the coefficients of the equation. We are looking for the value, or values, of the variable x for which the equation will be satisfied—that is, the left side of the equality will equal the right side.

The first transformation we perform when solving the equation is to move the coefficient b (which does not contain the unknown) to the right side of the equation, changing its sign (more precisely: we add −b to both sides of the equation). We get:

ax=−b

The next obvious transformation is to divide both sides of the equation by the coefficient a, so that only x remains on the left side. Before we do this, let's recall that the coefficient a is a fixed, known real number; specifically, it can be equal to 0, and we cannot divide by 0. Therefore, before performing the division, we must check if a is different from 0. If it is, we obtain the solution to our equation:

x=−b/a(a≠0)

The algorithm must also account for the case where a=0. In this situation, our equation looks like this:

0⋅x=−b

Of course, 0⋅x is always equal to 0 for every value of x, so we get:

0=−b

The left side of the above equality equals the right side only when b=0. Thus, when the coefficient a of the linear equation is equal to 0, we have two possible situations:

  • b=0: The equation is satisfied for every value of x (such an equation is called an identity equation and has infinitely many solutions).
  • b≠0: The equation is never satisfied (such an equation is called a contradictory equation and has no solution).

 

 

 

⚙️ The Final Algorithm (in English)

  1. Start: Read the coefficients a and b.
  2. Check if a is zero:
    • If a≠0:
      • Calculate the unique solution: x=−b/a.
      • Output the solution x.
    • If a=0: Go to step 3.
  3. Check if b is zero (when a=0):
    • If b=0:
      • Output the message: "The equation has infinitely many solutions (identity equation)."
    • If b≠0:
      • Output the message: "The equation has no solution (contradictory equation)."
  4. Stop.

 

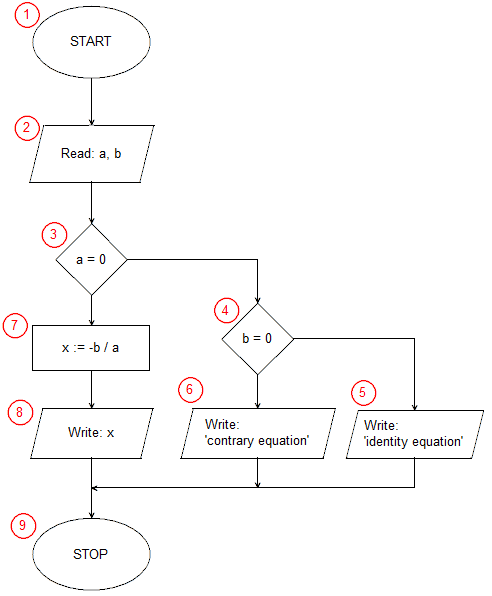
Ultimately, the algorithm for solving the linear equation ax+b=0, considering all possible cases, will look as follows:

 

example of an algorithm solving the linear equation

Implementation of the algorithm in the language: Pascal, C++, Java, Python, JavaScript

📝 Algorithm Description

  • Start - This is where our algorithm begins.
  • Read the input data - We read the equation coefficients a and b.
  • Check if the equation coefficient a is equal to 0.
  • If a=0, we check if the equation coefficient b is equal to 0.
  • b=0 - We output the information that the equation is an identity equation (infinitely many solutions).
  • b≠=0 - We output the information that the equation is a contradictory equation (no solution).
  • a≠=0 - We calculate the solution to the equation: x=−b/a.
  • a≠=0 - We output the result (the previously calculated value of x).
  • Stop - The common end point for all paths of the algorithm.

 

 

Facebook Twitter Linkedin