Prime number is a natural number greater than 1 divided by 1 and itself (eg 2, 3, 5, 7, 11 ...). Already the ancient Greek mathematician and philosopher Eratosthenes noted that the above definition of natural numbers can be formulated slightly differently, namely that the prime number is a natural number that is not a multiple of two other natural numbers greater than 1. This observation became the basis of his The algorithm for finding all natural numbers in the range of 2 to any given integer n.
The idea of the algorithm consists in deleting in the interval from 2 to n all multiples of consecutive numbers, Numbers that remain indefinite are not multiples of any other numbers in that range, so they are prime numbers.
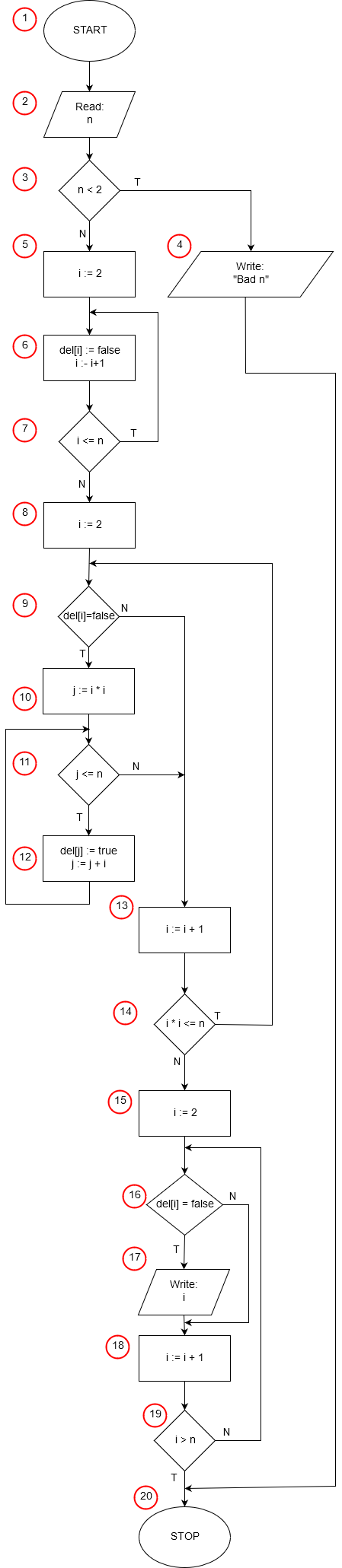
Implementation of the algorithm in: Pascal, C++, Java, Python, JavaScript
START - the beginning of the algorithm.
We Read: n (load the upper limit n of the range, from 2 to n, in which we will search for prime numbers). We check that n<2. The smallest prime number is 2. If n is less than two, we print out a message (e.g., "bad n") and STOP the algorithm (go to Point 20).
Initialization Phase (Points 5-7)
If n has a valid value, we begin the initialization. We initialize the boolean array, del (or skr), which stores information on whether a number has been deleted. Initially, no number is deleted. Therefore, in a loop corresponding to Points 5-7, we initialize all elements of the array from index 2 up to n with false values. We set the iterator i to 2, check if i≤n, set del[i]:=false, and then increment i by 1. When the condition (i>n) is no longer satisfied, the whole array is initialized, and we can begin the essential part of our algorithm.
Sieving Phase (Points 8-14)
At the beginning of this phase, we assign the iterator i a value of 2 (i:=2), which is the first number whose multiples we will mark.
We check whether the number i has been deleted (del[i]=false). If it has been deleted, it means all of its multiples have also been deleted by a smaller prime. In this situation, we go to Point 13 (increment i by 1) to check the next number.
If the number i has not been deleted so far, it is prime. We assign the multiple iterator j the value of i⋅i (j:=i⋅i). The smallest multiple we have to mark is i2, because all smaller multiples of i (e.g., 2i,3i,…) have already been deleted by their smaller prime factors.
We check the inner loop condition (Point 11): is j within the range (j≤n)? If the condition is not met (j>n), we go to Point 13; all necessary multiples of the current i are deleted.
If j≤n: We mark the element del[j] as deleted (del[j]:=true). We then increment the value of the variable j by i (j:=j+i) to get the next multiple, and return to Point 11.
After marking all multiples, we arrive at Point 13. We increase i by 1 (i:=i+1). We then check the main loop condition (Point 14): i∗i≤n. If true, we return to Point 9 to continue the sieving. If false, all possible multiples have been deleted, and the unmarked numbers are prime.
Output Phase (Points 15-20)
We need to check the values of all elements in the array del in turn and print out the numbers that were not deleted (del[i] is false). For this purpose, we initialize the iterator i with the value 2 (i:=2).
We check the condition in Point 16: Is the number i unmarked (del[i]=false)? If the condition is false (the number is deleted), we jump past Point 17 to Point 18.
If the number i is unmarked, we Write: i (print its value).
We increment i by 1 (i:=i+1). We check the condition in Point 19: Have we checked all numbers up to n (i>n)? If i≤n, we return to Point 16.
When the loop is finished, we reach Point 20 - STOP the algorithm.