Liczba pierwsza to liczba naturalna większa od 1 podzielna wyłącznie przez 1 i samą siebie (np. 2, 3, 5, 7, 11 ...). Już starożytny grecki matematyk i filozof Eratostenes zauważył, że podaną wyżej definicję liczb naturalnych można sformułować nieco inaczej, a mianowicie, że liczbą pierwszą jest liczba naturalna, która nie jest wielokrotnością dwóch innych liczb naturalnych większych od 1. To spostrzeżenie stało się podstawą opisanego przez niego algorytmu znajdowania wszystkich liczb naturalnych zawartych w zakresie od 2 do dowolnej określonej liczby całkowitej n.
Idea algorytmu polega na skreśleniu w przedziale od 2 do n wszystkich wielokrotności kolejnych liczb. Liczby, które pozostaną nieskreślone nie są wielokrotnościami żadnych innych liczb z tego zakresu, są więc liczbami pierwszymi.
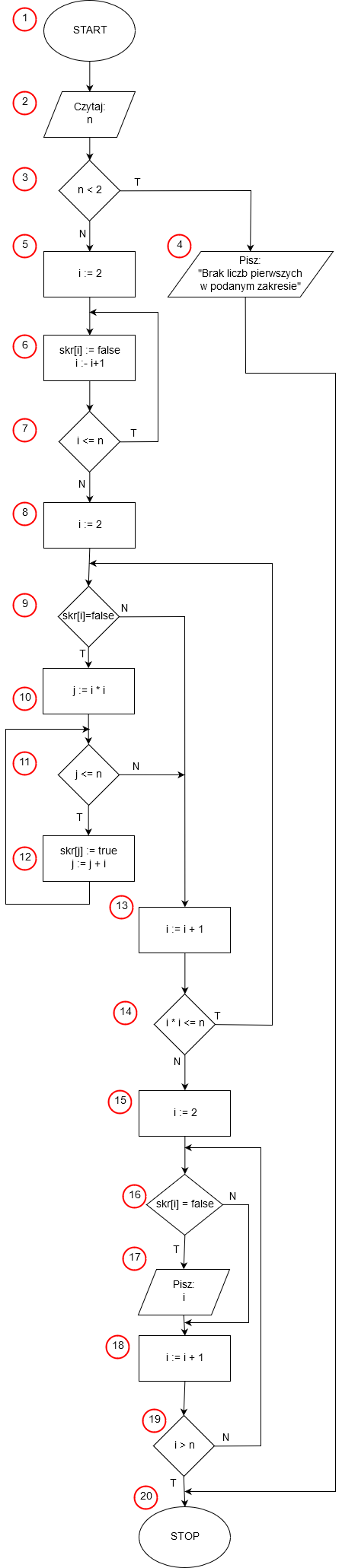 Realizacja algorytmu w języku: Pascal, C++, Java, Python, JavaScript
Realizacja algorytmu w języku: Pascal, C++, Java, Python, JavaScript
- START - początek algorytmu.
- Wczytujemy górną wartość zakresu, w którym będziemy poszukiwali liczb pierwszych (od 2 do n).
- Sprawdzamy, czy n nie jest mniejsze od 2. Najmniejszą liczbą pierwszą jest 2.
- Jeśli n jest mniejsze od dwóch wypisujemy komunikat informujący, że nie ma liczb pierwszych mniejszych od 2 i kończymy działanie algorytmu, idziemy do punktu 20 - STOP.
- Jeśli n ma prawidłową wartość przypisujemy do zmiennej i wartość 2.
- Elementowi o numerze i w tablicy skr przypisujemy wartość false (fałsz) i następnie zwiększamy wartość zmiennej i o 1. W tablicy skr przechowujemy informację, czy liczba o podanym numerze została w trakcie wykonywania algorytmu została skreślona. Początkowo żadna liczba nie jest skreślona, dlatego w punktach 5-7 inicjujemy wszystkie elementy tablicy wartościami false.
- Sprawdzamy czy i jest mniejsze lub równe n - górnej granicy poszukiwań. Jeśli warunek jest spełniony wracamy do punktu 6 naszego algorytmu, aby zainicjować wartość początkową kolejnego elementu tablicy.
- Gdy warunek z poprzedniego punktu nie jest spełniony (i jest większe od n) mamy zainicjowaną całą tablicę skr i możemy rozpocząć zasadniczą część naszego algorytmu. Na początek przypisujemy zmiennej i wartość 2, pierwszej liczby, której wielokrotności będziemy skreślali.
- Sprawdzamy, czy liczba o numerze i nie została już wcześniej skreślona. Jeżeli tak to znaczy, że i wszystkie jej wielokrotności również zostały już skreślone. W takiej sytuacji przechodzimy do punktu 13 algorytmu - zwiększamy i o 1, czyli sprawdzamy kolejną liczbę.
- Jeśli liczba nie została do tej pory skreślona to po pierwsze oznacza, że jest ona liczbą pierwszą i , po drugie, że należy skreślić wszystkie jej wielokrotności. Zauważmy, że wszystkie wielokrotności i poniżej i*i zostały skreślone już wcześniej. Np. dla i=5 10 zostało już skreślone podczas wykreślania wielokrotności 2, 15 zostało skreślone przy wykreślaniu wielokrotności 3, 20 wykreślono przy wykreślaniu wielokrotności 4. Pierwsza nie skreśloną jeszcze wielokrotnością 5 będzie 5*5: 25. Możemy w tym miejscu przypisać zmiennej j wartość i2 pierwszej nie wykreślonej jeszcze wielokrotności liczby i.
- Jeśli wartość zmiennej j numerującej skreślane wielokrotności liczby i mieści się w zakresie, w którym poszukujemy liczb pierwszych (jest mniejsza lub równa n) przechodzimy do punktu 12, w przeciwnym przypadku przechodzimy do punktu 13 naszego algorytmu - wszystkie wielokrotności bieżącej wartości i zostały skreślone i możemy zwiększyć wartość zmiennej i.
- W punkcie 12 znajdziemy się tylko wtedy gdy kolejna wielokrotność liczby i zawarta w zmiennej j mieści się w zakresie poszukiwań liczb pierwszych. Oznaczamy element o numerze j w tablicy skr jako skreślony (skr[j] := true) a następnie zwiększamy wartość zmiennej j o i, j staje się kolejną wielokrotnością i. Po zwiększeniu wartości j wracamy do punktu 11.
- Do tego miejsca dochodzimy za każdym razem gdy wykreślimy wszystkie wielokrotności liczby i. Zwiększamy i o 1, przygotowujemy się w ten sposób do skreślania wielokrotności kolejnej liczby.
- W punkcie 10 algorytmu zauważyliśmy, że najmniejszą wielokrotnością liczby i, którą musimy wykreślić jest i2. W tym punkcie sprawdzamy czy i*i<=n, czyli czy dla aktualnie osiągniętej wartości i pozostały jeszcze w badanym zakresie nieskreślone wielokrotności i. Jeśli tak wracamy do punktu 9 algorytmu - kontynuujemy wykreślanie. W przeciwnym przypadku stwierdzamy, że wszystkie możliwe wielokrotności liczb z zakresu od 2 do n zostały już skreślone - liczby, które pozostały nieskreślone są liczbami pierwszymi. W kolejnych punktach algorytmu wypiszemy je na ekranie.
- Aby wypisać znalezione wcześniej liczby pierwsze musimy sprawdzić po kolei wartości wszystkich elementów tablicy skr i wypisać numery tych, które nie zostały skreślone (skr[i] jest równe false). Kolejne elementy będziemy numerowali zmienną i, w tym celu inicjujemy ją wartością 2 - numer pierwszego elementu naszej tablicy.
- Sprawdzamy, czy liczba i pozostała nieskreślona. Jeśli warunek nie jest spełniony, czyli liczba jest skreślona, przeskakujemy do punktu 18 algorytmu przeskakując zawarte w punkcie 17 wypisywanie liczby pierwszej.
- Jeśli liczba i pozostała nieskreślona wypisujemy jej wartość - wartość zmiennej i, dla której element tablicy skr[i] ma wartość false.
- Zwiększamy o 1 wartość zmiennej i przechodząc do kolejnej liczby.
- Patrzymy, czy sprawdziliśmy już wszystkie liczby z zakresu od 2 do n. Jeśli nie wracamy do punktu 16.
- STOP - koniec algorytmu.