💻 Program Structure and Setup
In the first line of the program, we include the iostream (input-output streams) library header file. This is necessary because later in the program, we will want to be able to write to the screen (cout) and read input from the keyboard (cin).
In the second line, we include the iomanip library header file, which we will use for formatting output data.
The third line informs the compiler that we will be using names defined in the std namespace in the program (these will be: cin, cout, endl, setw). If we didn't do this, it would be necessary to use the longer form of qualified names (std::cin, std::cout, std::endl, std::setw).
In the next line, we define an integer constant MAX, which specifies the maximum upper bound of the interval in which we will be searching for prime numbers. The lower bound is always 2. How high the value of the constant MAX can be depends on the compiler we are using and the amount of RAM available to the program.
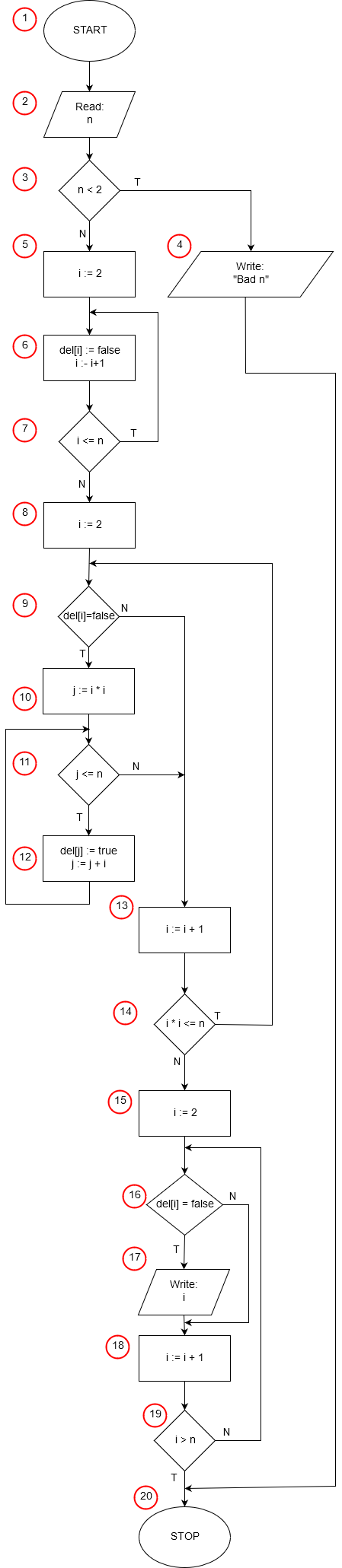
In C++, a program begins with the execution of the main function. In our example, this is the program's only function. Line 6 contains the start of the main function definition; this is the beginning of the realization of our algorithm (the START block (1)).
In the next line, we declare the integer variable n, which we will be using shortly. In C++, variables can be declared anywhere before their use, which is why we do not immediately declare the variables i, j, del here, as they might not be needed at all.
📥 Input and Validation
Lines 8 and 9 perform an input/output operation (2), in which the input data – the upper bound of the range for finding prime numbers – is retrieved.
In line 10, we check whether we have enough space in the del array to execute the rest of the algorithm. If n>MAX, it means that the entered number exceeds the allowed range for storing the sieve information (del stands for deleślenie or "sieve/cross-out") stored in the del array. In this case, we print an appropriate message and do not continue executing the algorithm.
Otherwise (the else keyword), if the value of n is not too large, we check in line 11 if n is not too small (it cannot be less than 2) – point (3) of the algorithm. In such a situation, we also print a message about the incorrect value (4) and do not continue executing the algorithm.
In line 12, the else keyword appears again. This else refers to the second if statement (from line 11). In C++, exactly one statement can follow the else keyword, which is executed when the condition in the if statement was not met. If we want to include more statements here, we must enclose them in curly braces {…} (often called logical braces). In line 12, after the else keyword, we placed an opening brace { starting the sequence of statements to be executed when a valid value was entered into the variable n. This sequence of statements is finally closed by the closing brace on line 27 of the program.
⚙️ Sieve Algorithm Implementation
In the subsequent part of the program, we will use the del array to store boolean logic values. We declare it in line 13 before use. When declaring an array variable, we must specify the number of array elements in square brackets placed after the variable name. In C++, array element numbering always starts from 0. If we want the number of the last element to be MAX, we must declare an array with MAX+1 elements.
Points (5) to (7) of our algorithm can be read as: starting from the element with index 2 up to the element with index n, assign the boolean value false to consecutive elements of the del array. The realization of these three points of the algorithm is contained in line 14 of the program. We set the lower bound of the variable i (the for loop control variable) to 2 (for(int i=2… – we declare and initialize the variable i, controlling the execution of our loop; the variable i declared here exists only within the scope of the loop), and the upper bound to n (…,i<=n…). After the organizational part of the loop, there is the instruction executed sequentially for each value of i: del[i]:=false. In this way, we have initialized all elements of the del array used by the algorithm with the boolean value false. It is worth noting here that if n<MAX, we do not use the entire del array in the program, but only its first n elements, and we only initialize these elements; the rest are irrelevant to us. The first two elements of the array (del[0] and del[1]) also remain unused.
In line 15, we declare two helper variables: i and j. Simultaneously, in accordance with point (8) of the algorithm, we assign the value 2 to the helper variable i. The variable i created here has nothing to do with the variable of the same name used to control the loop in line 14. That variable was declared inside the for loop and only existed within that loop; after the execution of the for statement was completed, it was "forgotten" and released.
Points (9) to (14) of the algorithm can be read as: for successive values of the variable i starting from 2, cross out all multiples of i. Cross out until i satisfies the condition: i⋅i>n, or, in other words, cross out as long as i⋅i≤n. In C++, the instruction implementing the pattern "execute while the condition is met" is the do…while loop:
do instruction while (condition);
The execution of the instruction contained between the keywords do and while is repeated as long as the condition after the word while is met. The fulfillment of this condition is checked after each execution of the instruction; the instruction will be executed at least once (before the first check of the condition). When the condition is not met, the program does not return to the beginning of the loop but proceeds to execute the rest of the program located after the do…while loop condition. If we have more than one instruction to execute in the loop, we enclose them in curly braces.
In line 16, we start our do…while loop with the keyword do and open a curly brace, in which we will place the instructions executed in the loop.
In line 17, we check whether the number i has not been crossed out before (9). The condition if (!del[i]) is satisfied when del[i] contains the value false, which means that the number i has not been crossed out so far (it is a prime number) and we must cross out all its multiples. The first multiple that must be crossed out has the value i2 (in line 18, we assign j:=i⋅i) (see the justification in the algorithm description) – point (10) of the algorithm.
Points (11) - (12) of the algorithm can be read as: as long as j≤n, cross out the number j and then increase the value of j by i (assign the next multiple of i to j). In C++, the instruction implementing the pattern "while the condition is met, execute the instruction" is the while loop:
while (condition) instruction;
As long as the condition written after the while keyword is met, execute the instruction. Traditionally, if we need to place more instructions here, we must enclose them in logical braces {}.
In line 19, we start a while loop that will be executed for all values of j less than or equal to n. Lines 20 - 21 contain the instructions executed in the loop within braces {}. In line 20, we assign the value true to the element with index j of the del array (we cross out j), and then in line 21, we increase the value of j to the next multiple of i – point (12) of the algorithm. In line 22, we close the curly brace from line 19.
In line 23, we close the curly brace started in line 17 after the if statement checking if the number has not been crossed out before.
In line 24, we implement point (13) of the algorithm: we increase i by 1, thus preparing for crossing out the multiples of the next number.
Line 25 ends the do…while loop, in which we cross out all multiples of consecutive numbers. It contains the loop continuation condition i⋅i≤n. When the condition is not met (there is nothing left to cross out), the program finishes executing the loop, and we proceed to the instruction contained in line 26. When the condition is met, we return to the beginning of the loop at line 17.
In line 26, we print in a for loop all numbers in the range from 2 to n that have not been crossed out (!del[i]) – the prime numbers.
The curly brace } on line 27 ends the conditional statement from line 11, specifically the part contained after the else keyword from line 12.
🛑 Program End
The instructions in lines 28 - 30 have no connection with the execution of the division algorithm. They serve to pause the program until any character is entered and the enter key is pressed, which prevents the program window from closing immediately.
The curly brace } on line 31 ends the main function and simultaneously the operation of the entire program (the END block (20) of the algorithm).