The algorithm is a recipe for performing a specific task. With algorithms, we meet in everyday life at every step, often without realizing it.
In the morning, we brush our teeth by roughly following the scheme below:
- squeeze a small amount of toothbrush paste,
- brush your teeth for 2 minutes,
- rinse your mouth a few times with water,
- wash the brush under running water.
Later, we prepare our favorite scrambled eggs for breakfast, also realizing the well-known recipe:
- put some fat on the pan, eg butter,
- lighting the oven burner,
- place the pan with fat on the burner,
- pour 3 eggs into the pan, throw the shells in the basket,
- pour in two pinches of salt,
- stirring wait until the contents of the pan thickens,
- turn off the burner,place the pan on the plate and eat it.
In a similar way, you can describe dozens of activities performed every day, or provide algorithms for their implementation. Each of these rules tells us how a certain initial state of a particular system can be transformed into the desired final state (dirty teeth -> clean teeth, raw eggs -> scrambled eggs).
In mathematics and informatics, we also call the algorithm a recipe that tells us how to do a certain task, achieve a specific goal. At the same time, however, we formulate to this provision some strictly defined requirements that must be met in order to be called an algorithm:
The algorithm is an orderly, finite sequence of unambiguously defined activities whose completion in a finite period leads to the solution of the task.
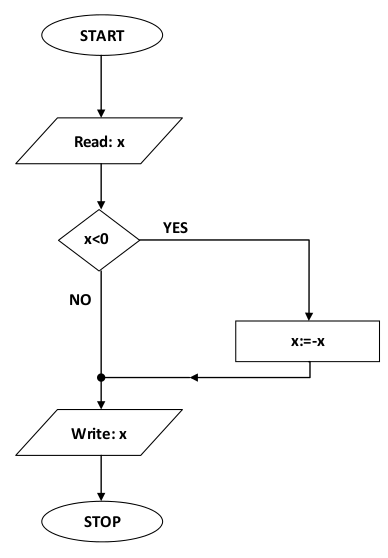
An example of a mathematical algorithm, finding the absolute value of a number
- Load x
- Is x <0?
- If YES: x: = - x (change the sign to positive)
- If NO: do nothing
- Write x (the absolute value of the number loaded)
Ways of writing the algorithm
The algorithms can be presented in various ways: descriptively, in points (so we have done so far), using the instructions of the chosen programming language or graphically, using generally accepted symbols. The latter method is very popular, Below are the symbols that we will use to write the algorithms:
The beginning of the algorithm. The origin symbol of the algorithm occurs exactly once. No arrow comes from him, and one goes out.
The end of the algorithm. The symbol of the end of the algorithm, just like the start symbol, must occur in the algorithm once. No arrow comes out of it, and at least one goes.
The input or output block of the algorithm. It presents the action of entering data into the algorithm (eg read: x), as well as outputting the results and messages received (eg, write: y * 5). With an input/output block, exactly one incoming and one outgoing arrow is associated.
The operating block contains operations performed by the algorithm. The operating blocks contain all calculations performed during the implementation of the algorithm. Each operating block has exactly one incoming arrow and exactly one outgoing arrow.
Decision block, otherwise conditional. Inside the block, we place a condition that can be met or not. If the condition is satisfied, we leave the block with the way described "YES", while if the condition is false, we continue along the path marked with an arrow described as "NO". One entry arrow comes to the decision block and two exit arrows exit ("YES" and "NO").
Once we have learned the symbols used to graphically present the algorithms, we can draw the previously described algorithm for finding the absolute value of the number: