Eratosthenes sieve in Python

<<algorithm

n = int(input('n = '))
if n < 2:
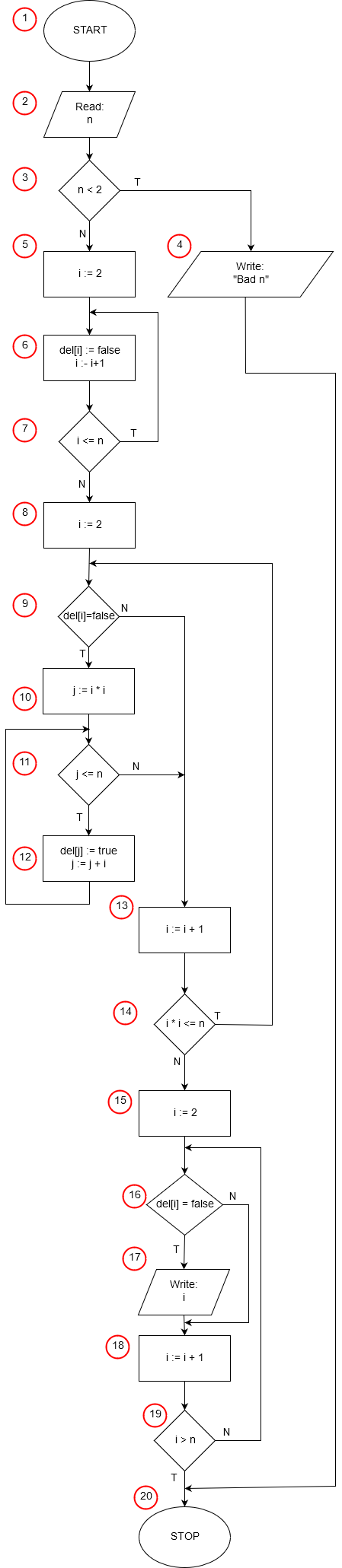
    print("No prime numbers in the given range")
else:
    deleted = [False] * (n + 1)
    i = 2
    while i * i <= n:
        if  not deleted[i]:
            j = i * i            
            while j <= n:
                deleted[j] = True
                j += i
        i += 1
    for i in range(2, n+1):
        if not deleted[i]:
            print(i, end = " ")

Line Number	Algorithm Step (Flowchart)	Description	Notes
-	1	START	Program start.
1	2	Read: n	Inputting the upper limit n.
2	3	n < 2	Checking the initial condition.
3	4	Write: "bad n"	Output message if n < 2.
4	-	else	Block execution starts for n >= 2.
5	6	del[1..n] := false	Initialization of the boolean array deleted.
6	5	i := 2	Initialization of the iterator i.
7	7	i * i < n	Main Sieve Loop.
8	9	del[i] = false	Check if i is prime (if not deleted[i]:).
9	8	j := i * i	Initialization of j to the square of i.
10	11	j < n	Inner loop condition (for marking multiples).
11	-	Blank line/start of inner loop body	Corresponds to the entry of the loop body.
12	10	deleted[j] := true	Marking the multiple j as composite1.
13	12	j := j + i	Moving to the next multiple 2.
14	13	i := i + 1	Incrementing i to the next candidate number.
-	-	Blank line/end of the main loop	End of the while i * i <= n: block.
15	15	i := 2	Output Loop (for i in range(2, n+1):).
16	16	del[i] = false	Checking if i is prime (if not deleted[i]:).
17	17	Write: i	Outputting the prime number.
-	18	i := i + 1	Increment performed by the for loop structure.
-	19	i > n	Exit condition for the output loop.
-	20	STOP	Program termination.