Sito Eratostenesa w Pythonie

n = int(input('n = '))
if n < 2:
    print("Brak liczb pierwszych w podanym zakresie")
else:
    skr = [False] * (n + 1)
    i = 2
    while i * i <= n:
        if  not skr[i]:
            j = i * i            
            while j <= n:
                skr[j] = True
                j += i
        i += 1
    for i in range(2, n+1):
        if not skr[i]:
            print(i, end = " ")

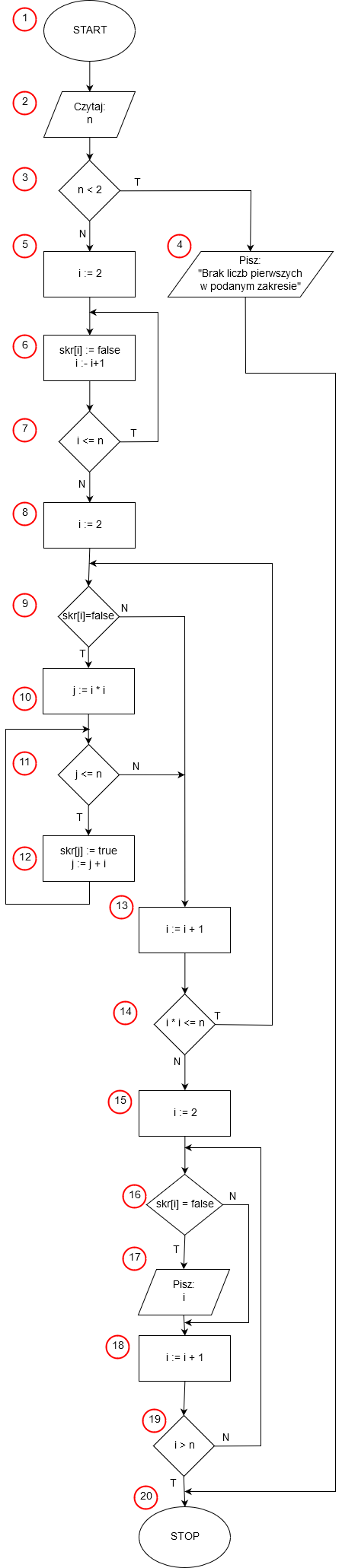
Numer Linii	Punkt Algorytmu	Opis Punktu	Uwagi
-	1	START	Początek programu.
1	2	Czytaj n	Wczytanie granicy zakresu n.
2	3	n < 2	Sprawdzenie warunku początkowego.
3	4	Pisz: "Brak liczb pierwszych..."	Komunikat dla n < 2.
4	-	else	Blok wykonawczy dla n >= 2.
5	6	skr[1..n] := false	Inicjalizacja tablicy skr (skreślenia).
6	5	i := 2	Inicjalizacja iteratora i (logicznie następuje po inicjalizacji tablicy, choć numeracja na schemacie jest inna).
7	7	i * i < n + 1	Główna pętla sita. Warunek i * i <= n.
8	9	Brak odpowiednika	Sprawdzenie, czy i jest liczbą pierwszą (if not skr[i]:).
9	8	j := i * i	Inicjalizacja j na kwadrat liczby i.
10	10	j < n + 1	Pętla wewnętrzna. Warunek j <= n.
11	11	skr[j] := true	Oznaczenie wielokrotności j jako złożonej.
12	12	j := j + i	Przejście do następnej wielokrotności.
13	13	i := i + 1	Przejście do następnej liczby kandydującej.
14	15	i := 2	Pętla wypisująca wyniki (for i in range(2, n+1):).
15	16	skr[i] = false	Sprawdzenie, czy i jest pierwsza (if not skr[i]:).
16	17	Pisz: i	Wypisanie liczby pierwszej.
-	18	i := i + 1	Wykonanie przez pętlę for.
-	19	i > n	Koniec pętli for.
-	20	STOP	Koniec programu.