Zauważmy, że
n! = 1 * 2 * ... * (n - 1) * n = (n - 1)! * n
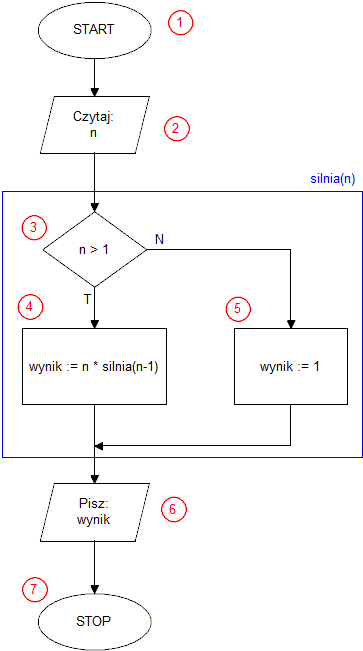
Dla n>1 silnia z n jest równa silni z n-1 pomnożonej przez n. Taki sposób zdefiniowania funkcji poprzez wartość tej samej funkcji liczonej dla zmienionej (najczęściej zmniejszonej) wartości argumentu tej funkcji nazywamy rekurencją. Inaczej mówiąc z rekurencyjną definicją funkcji mamy do czynienia wtedy, gdy w definicji pojawia się ta sama funkcja. Oczywiście obliczając silnię z jakiejś liczby całkowitej nie możemy w nieskończoność wywoływać funkcji silnia dla kolejnych algorytmów. Algorytm musi zostać zrealizowany w skończonej liczbie kroków. Musi istnieć jakaś wartość argumentu, dla której zamiast kolejnego wywołania funkcji otrzymamy jakąś konkretną wartość. W przypadku funkcji silnia tą wartością jest 1, 1!=1.
Definicję funkcji silnia, którą napisaliśmy na wstępie musimy uzupełnić o warunek przerywający rekurencję, otrzymując ostatecznie:
n! = 1 * 2 * ... * (n - 1) * n = (n - 1)! * n dla n>1
1! = 1
Realizacja algorytmu w języku:Pascal, C++, Java, Python, JavaScript