Silnia w pascalu - rekurencyjnie

program factorial_rek;

function factorial(n: integer): integer;
begin
  if n>1 then
    factorial:=n*factorial(n-1)
  else
    factorial:=1;
end;

var n, f: integer;
begin
  write('n = ');
  readln(n);
  f:=factorial(n);
  writeln(n,'! = ',f);
  readln;
end.

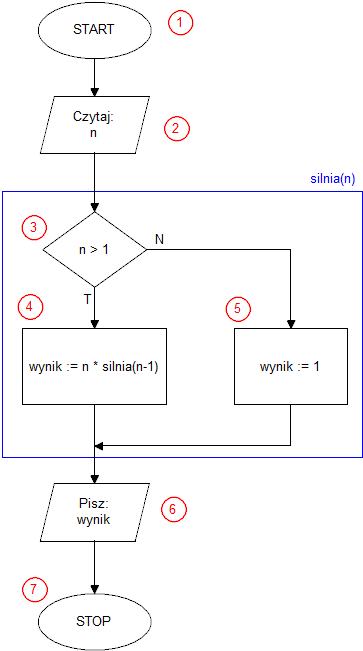
The first line of the program can be treated as an embellishment, yet it is required by the Pascal language syntax. Every Pascal program must start with the keyword program preceding the program's name, and it contributes nothing to the algorithm's execution.

In the third line, we declare a function named factorial, which accepts one integer parameter (n) and returns an integer result. The function body—the set of instructions executed by the program after the function is called—is contained between the keywords begin on line 4 and end on line 9.

In line 5, we check if n is greater than 1—block (3) of the algorithm. If so, then in line 6, we set the function's result as n multiplied by the value of the factorial function (the same factorial function we are currently defining) for n minus 1 (4). At this point, the factorial function calls itself. Such a function is called a recursive function. If n is not greater than 1, then in line 8 we set the function's result equal to 1 (the condition for ending the recursion)—block (5).

Before starting the operational part of the program, in line 11, we declare two integer variables (n and f (result)). In Pascal, all variables must be declared before the start of the code block. When declaring a variable, we must specify the type of data it will store. The declaration of variables begins with the keyword var.

Line 12, containing the keyword begin, corresponds to the START block (1) of our algorithm.

Lines 13 and 14 implement the input/output operation (2), where the input data is retrieved—the number n whose factorial we want to calculate.

In line 15, we assign the result of the factorial function, called with the argument n, to the variable f.

In line 16, we print the obtained result (input-output block (6)).

The readln instruction on line 17 has no relation to the execution of the algorithm. It serves to pause the program until the Enter key is pressed, which prevents the program window from closing immediately.

The instruction end. on line 18 concludes the program's execution (the algorithm's STOP block (7)).